Capítulo 2 Filtragem

As técnicas de filtragem se dividem em filtragem espacial e filtragem no domínio da frequência (R. C. GONZALEZ 2010). Serão tratados aqui filtros espaciais, que são implementados no domínio espacial, que se trata do plano que contém os pixels, já os filtros do domínio da frequência são aplicados sobre a Transformada de Fourier de uma imagem, e não sobre a imagem em si (R. C. GONZALEZ 2010). Filtros espaciais podem ser descritos pela Equação (2.1):

\[\begin{equation} g(x,y)=T[f(x,y)] \tag{2.1} \end{equation}\]

onde \(f(x,y)\) é a imagem de entrada, \(g(x,y)\) é a imagem de saída, e \(T\) é um operador em \(f\) definido em uma vizinhança do ponto \((x,y)\) (R. C. GONZALEZ 2010).

Um dos princípios da filtragem é que para atribuir um novo valor para o pixel \((x,y)\) leva-se em consideração não só o pixel analisado, mas também o seu entorno. Um filtro pode ser definido pelo seu aplicador (também chamado de máscara), que é o que define como será utlizado o entorno do pixel para gerar \(g(x,y)\). Normalmente este aplicador é retangular e bem menor do que a imagem (R. C. GONZALEZ 2010). A filtragem pode ser explicada melhor analisando o processo de convolução, que é o processo de aplicação da máscara do filtro.

2.1 Convolução

O processo de convolução pode ser realizado tanto de forma unidimensional, bidimensional, cúbica, etc. Os filtros aplicados em imagens digitais orbitais se tratam normalmente de processos de convolução bidimensional. O processo pode ser descrito como parte integrante da função \(T\) da equação (2.1), onde o espaço da imagem é percorrido pela máscara definidora do filtro. A Figura 2.1 demonstra como uma máscara de ordem 3 x 3 percorre uma imagem para a aplicação do filtro (P. R. MENESES 2012).

Figura 2.1: Movimento da máscara de tamanho 3 x 3 para filtrar a imagem. O pixel cinza é o pixel central que terá o seu valor modificado conforme sejam os pesos dos pixels do filtro. Fonte: (P. R. MENESES 2012)

O pixel cinza central, demonstrado na Figura 2.1, é o pixel que está sendo filtrado e as linhas mais escuras representam a sobreposição da máscara com o entorno do pixel central. Seu novo valor é obtido a partir da combinação dos valores da máscara e do pixel central e sua vizinhança sobreposta. De acordo com (O. MARQUES FILHO 1999), o processo de obtenção de um novo valor para o pixel filtrado pode ser definido da seguinte forma:

Sendo o seguinte arranjo uma máscara 3 x 3 de um filtro qualquer de coeficientes genéricos \(W_1\), \(W_2\), …, \(W_9\):

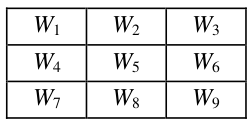
Figura 2.2: Máscara genérica 3 x 3 de um filtro.

E o seguinte arranjo uma sub-área de uma imagem, recoberta pela máscara anterior em um dos passos da Figura 2.1, com valores de níveis de cinza iguais a \(Z_1\), \(Z_2\), …, \(Z_9\)

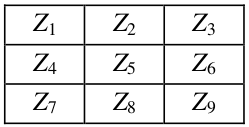
Figura 2.3: Sub-área coberta pela máscara do filtro.

A máscara percorre toda a imagem a partir do canto superior esquerdo até o canto inferior direito, definindo a cada posição uma nova sub-imagem para a filtragem do pixel referente à posição \(Z_5\) (o pixel central, cinza na Figura 2.1. O valor do pixel filtrado referente a cada posição da máscara é salvo em uma matriz denominada de “imagem-destino”, por um valor correspondente a Equação (2.2) (O. MARQUES FILHO 1999).

\[\begin{equation} Z = \sum\limits_{i=1}^9(W_i \cdot Z_i) \tag{2.2} \end{equation}\]

Criando arranjos de coeficientes para as máscaras de forma inteligente, podem ser obtidos os mais diversos filtros e efeitos na imagem filtrada. Dentro deste escopo, podem ser citados dois tipos de filtros: filtros passa-baixa e filtros passa-alta.

2.2 Filtros Passa-Baixa

Filtros passa-baixa são aqueles que preservam os componenetes de baixa frequencia da imagem, removendo ruídos à custo da nitidez, portanto, podem ser considerados filtros de suavização (P. R. MENESES 2012). Por suavizar a imagem, detalhes como bordas ríspidas (diferenças abruptas dos níveis de cinza entre pixels vizinhos) tendem a serem atenuadas, o que também acontece com os ruídos provenientes das mais diversas fontes, como erros no obturador, atmosfera, etc. Uma característica marcante de tais filtros, é que a máscara possui apenas termos com valor maior ou igual a zero. Exemplos clássicos de filtros passa-baixa são o Filtro de Média, Filtro de Mediana e Filtro Gaussiano.

2.2.1 Filtro de Média

Este filtro é definido por ter em todos os termos da máscara o valor 1. Se trata, literalmente, de implementar a média da região coberta pela máscara para o novo valor do pixel filtrado.

A Figura 2.4 ilustra uma máscara de ordem 3 x 3 para o filtro de média.

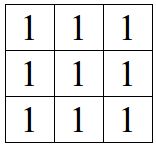
Figura 2.4: Exemplo de máscara de ordem 3 x 3 para o Filtro de Média, sendo o termo do centro relativo ao pixel filtrado.

Tal filtro possui uma das implementações mais básicas para um filtro, podendo este ser usado no âmbito desta biblioteca através da função filter_mean( ). O efeito deste filtro em uma imagem sintética pode ser visto na Figura 2.5, a seguir.

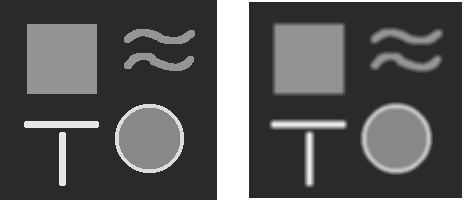
Figura 2.5: Exemplo de aplicação do Filtro de Média em uma imagem sintética.

2.2.2 Filtro da Mediana

Durante o processo de convolução, são usados como dados de entrada os valores dos níveis de cinza correspondentes ao espaço recoberto pela máscara. O que diferencia os filtros de PDI são justamente as formas com que tais dados são tratados para que se obtenha o novo valor para o pixel analisado.

No Filtro da Mediana, busca-se dentro do intervalo de dados, oriundos do recobrimento da máscara, pelo valor mediano dos níveis de cinza, sendo este o novo valor a ser adotado pelo pixel filtrado.

Considerando como exemplo o conjunto de dados da Figura 2.6, têm-se que os dados ordenados de forma crescente são: 3, 27, 55, 92, 177, 196, 208, 212 e 237.

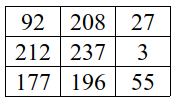
Figura 2.6: Exemplo de intervalo de dados referentes a níveis de cinza recobertos por uma máscara 3 x 3 para a filtragem do elemento correspondente ao número 237.

Sendo assim, o pixel de valor correspondente a 237 passa a ser igual a 177, por este ser o valor da mediana para a janela observada. O filtro tem alto potencial de uso principalmente em casos onde há ruído de “sal e pimenta” nas imagens, como descrito por (R. C. GONZALEZ 2010).

Tal filtro pode ser usado no contexto desta biblioteca através da função filter_median( ), e seu efeito pode ser visto através da Figura 2.7.

Figura 2.7: Exemplo de aplicação do Filtro da Mediana em uma imagem sintética com ruído. Imagem original (a); Imagem (a) corrompida por ruído “sal e pimenta” (b); e Aplicação do Filtro de Mediana (c).

2.2.3 Filtro Gaussiano

A Filtragem Gaussiana é um processo onde a convolução é realizada na imagem visando a suavisação da cena, com uma máscara construída de forma condizente com a distribuição normal bidimensional. Gonzalez e Woods (2010) destacam que uma das formas de se implementar um filtro gaussiano é definindo a máscara através da Equação (2.3), onde a máscara final sofre uma normalização, para que assim a soma de seus elementos seja igual a 1.

\[\begin{equation} h(x,y) = e^{-\frac{x^2+y^2}{2\sigma^2}} \tag{2.3} \end{equation}\]

Onde \(x\) e \(y\) são a distância do centro da máscara, medidos em unidades de pixel, já \(\sigma\) é o desvio padrão utilizado para a distribuição, definindo o abaolamento do “sino” fomado pela distribuição.

Diferentes valores de \(\sigma\) geram diferentes “sinos” para a distribuição normal. Quanto maior o valor de \(\sigma\) usado, maior será o abaolamento, levando a um maior borramento da imagem. A Figura 2.8 demonstra o formato da distribuição dos pesos da máscara de acordo com o valor de \(\sigma\) adotado.

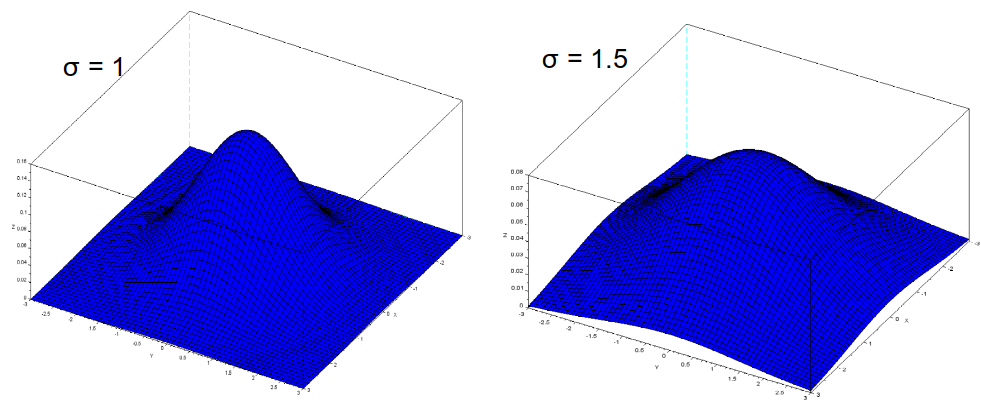
Figura 2.8: “Sinos” gerados pela distribuição normal a serem usados na definição da máscara do Filtro Gaussiano, usando sigma igual a 1 e 1.5.

Um exemplo da aplicação do Filtro Gaussiano pode ser encontrado na Figura 2.9, a seguir:

Figura 2.9: Exemplo de aplicação do Filtro Gaussiano em uma imagem sintética com ruído radiométrico. Imagem sintética original (a); Imagem sintética com ruído radiométrico (b); e Aplicação do Filtro Gaussiano (c).

2.3 Filtros Passa-Alta

De acordo com (R. C. GONZALEZ 2010), diferente dos filtros passa-baixa, os filtros passa-alta têm um efeito de realce nas imagens, aumentando a nitidez de detalhes abruptos, porém, provocando uma redução no contraste da imagem.

Os filtros passa-alta são compostos da mesma forma que qualquer outro outro tipo de filtro: são definidos pela máscara usada no processo de convolução. Tal máscara aqui pode ter termos positivos, negativos, ou nulos. Outros tipos de filtros, como a detecção de bordas, também são passíveis de implementação, visto que os termos da máscara podem assumir valores que os filtros passa-baixa não o fazem.

A possibilidade de aumentar a nitidez de imagens através destes tipos de filtros é muito vantajosa, porém, tais filtros realçam também o ruído, que acaba por atrapalhar a interpretação das cenas.

Um dos filtros passa-baixa mais conhecidos é o Operador de Sobel.

2.3.1 Operador de Sobel

A magnitude do gradiente são usadas em PDI para a implementação das derivadas de primeira ordem. A euquação a seguir mostra que o gradiente de \(f\) nas coordenadas \((x,y)\) de uma função \(f(x,y)\) é definido como o vetor coluna bidimensional dado na Equação (2.4) (R. C. GONZALEZ 2010).

\[\begin{equation} \bigtriangledown f \equiv grad(f) \equiv \left [ \begin{matrix} g_x\\ g_y \end{matrix} \right ] = \left [ \begin{matrix} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y} \end{matrix} \right ] \tag{2.4} \end{equation}\]

A principal propriedade geométrica deste vetor é a de apontar na direção da maior taxa de variação de \(f\) na posição \((x,y)\). O módulo do vetor \(\bigtriangledown f\) é escrito como \(M(x,y)\), de acordo com a Equação (2.5).

\[\begin{equation} M(x,y)=mag(\bigtriangledown f)=\sqrt{g^2_x+g_y^2} \tag{2.5} \end{equation}\]

Neste caso, \(M(x,y)\) é o valor da taxa de variação na direção do vetor gradiente.

De uma forma mais simples, o Operador de Sobel pode ser descrito em duas etapas:

• A aplicação de duas diferentes máscaras na mesma imagem, resultando em \(g_x\) e \(g_y\) - imagens de mesmo tamanho, como mostrado na Figura 2.10.

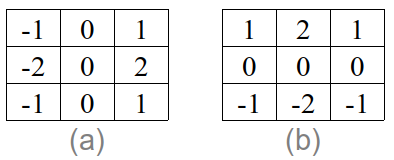
Figura 2.10: Máscaras usadas pelo Operador de Sobel para compor \(g_x\) (a) e \(g_y\) (b).

• Depois disso, cada termo \(a_{ij}\) da imagem resultante é calculado pela Equação (2.6):

\[\begin{equation} a_{ij} = \sqrt{{g_{x_{ij}}}^2+{g_{y_{ij}}}^2} \tag{2.6} \end{equation}\]

Um exemplo para a aplicação do Operador de Sobel pode ser encontrado na Figura 2.11.

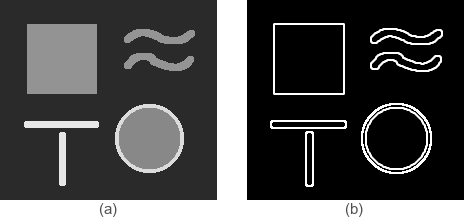
Figura 2.11: Imagem sintética (a); e Aplicação do Operador de Sobel (b).

Como visto na Figura 2.11 o efeito alcançado pelo Operador de Sobel é referente a detecção das bordas das feições presentes na imagem digital. Mais detalhes sobre a detecção de bordas são apresentados na Seção 5 - Detecçöao de Bordas deste material.

Tal método pode ser mudado para que bordas apenas em certas direções sejam adiquirias, mais especificamente, nas direções Norte-Sul, Leste-Oeste, Noroeste-Sudeste, e Nordeste-Sudoeste. Para tal, basta usar as seguintes máscaras no processo de filtragem, de acordo com a Figura 2.12.

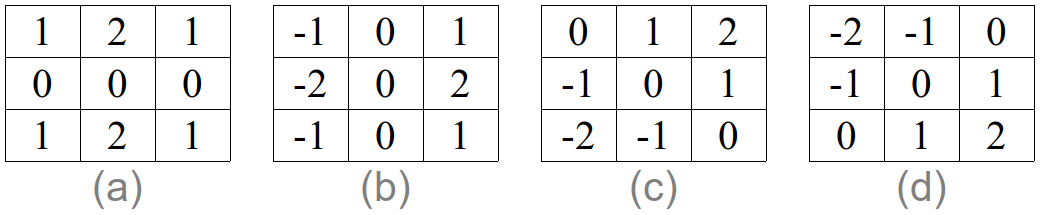
Figura 2.12: Máscara para bordas nas direções Norte-Sul (a), Leste-Oeste (b), Noroeste-Sudeste (c), e Nordeste-Sudoeste (d).

O Operador de Sobel pode ser usado nesta biblioteca por meio da função filter_sobel( ).

2.4 Filtragem Adaptativa

A meta dos filtros adaptativos é transformar os sinais portadores de informação em um produto mais “limpo”, mais aprimorado. Tais filtros possuem regulação dinâmica, adaptando-se de acordo com os sinais encontrados. Tais tipos de filtros posem ser considerados um exemplo simples de algoritmos nda área de aprendizado de máquinas (P. A. REGALIA 2005).

Nos filtros elucidados anteriormente, têm-se sempre uma máscara fixa definida pelo usuário que filtra de forma constante e estática toda a imagem, uniformemente. No caso dos filtros adaptativos os parâmetros de filtragem de uma imgagem são calculados de acordo com dados estatísticos extraídos da mesma. Um exemplo de filtro adaptativo desenvolvido pelos autores e presente neste pacote é o Filtro Gaussiano Adaptativo.

2.4.1 Filtro Gaussiano Adaptativo

No âmbito desta bibilioteca foi implementado um Filtro Gaussiano Adaptativo. No Filtro Gaussiano convencional uma máscara é definida no início do processo de filtragem de acordo com um valor de \(\sigma\) aplicado à distribuição normal, e esta máscara percorre toda a imagem com todos os seus valores permanecendo os mesmos durante todo o processo - A imagem é filtrada toda pela mesma máscara. A estratégia escolhida para a implementação do Filtro Gaussiano Adaptativo foi implementar o filtro de forma que uma nova máscara fosse gerada para ser usado no processo de filtragem de cada pixel, usando as estatísticas dos valores sobrepostos na imagem pela máscara para definir o valor de \(\sigma\) a ser usado na distribuição normal.

O objetivo de tal filtro é diminuir o ruído das imagens orbitais no interior de feições, porém, mantendo intactas as bordas das mesmas, uma vez que o Filtro Gaussiano convencional diminui este ruído, porém, compromentendo a informação das bordas dos elementos da cena, como pode ser visto na Figura 2.9.

Como dito anteriormente, ao usar um maior valor de \(\sigma\) no Filtro Gaussiano convencional, obtém-se um maior borramento dos elementos da imagem, o que é desejável para as áreas internas das feições, que normalmente são homogêneas, e indesejável para as áreas de bordas de objetos, os quais deseja-se manter intactos.

Tomando isso em consideração, analisa-se o comportamento estatístico das áreas de borda e das demais áreas. Para os casos onde há a presença de bordas, o desvio padrão entre os níveis de cinza tende a ser alto, devido à discrepância dos mesmos que formam a borda. Já para os demais casos, mesmo com ruído onde não há a presença de bordas, o desvio padrão mostra-se de menor magnitude que em regiões de bordas, portanto, para que tal filtro “borre” áreas internas de feições com ruído e mantenha as bordas intactas, adotata-se o inverso do desvio padrão da área do pixel filtrado para que seja criada a máscara a ser usada na filtragem do mesmo. A Figura 2.13 mostra o resultado da aplicação de tal filtro em uma imagem sintética corrompida por ruído.

Figura 2.13: Exemplo de aplicação do Filtro Gaussiano em uma imagem sintética com ruído radiométrico. Imagem sintética original (a); Imagem sintética com ruído radiométrico (b); e Aplicação do Filtro Gaussiano Adaptativo (c).

Como pode ser visto, o interior das figuras foi filtrado com sucesso, enquanto a informação das bordas foi mantida praticamente intacta. No contexto desta bibilioteca, tal função pode ser usada através de filter_gauss_localsigma( ), sendo os parâmetros de entrada a imagem a ser filtrada, o tamanho da máscara (opcional, padrão igual a 3), e o numerador a ser usado no inverso do desvio padrão a ser usado como \(\sigma\) na distribuição normal (opcional, padrão igual a 0,05).

2.5 Exercícios

1. O que é uma máscara no contexto do PDI?

2. Para se filtrar um pixel, é necessário apenas a máscara e o pixel a ser filtrado? Por quê?

3. O que é o processo de convolução?

4. Considere a seguinte máscara cujo termo central é referente ao pixel a ser filtrado:

0.98	0.10	0.89
0.03	0.91	0.11
0.78	0.00	0.99

Considere então o seguinte conjunto de pixels:

100	88	44
114	102	82
130	115	99

Considerando que a imagem aceita apenas valores inteiros como pixel, qual deve ser o novo valor do pixel central para a aplicação desta máscara no trecho de imagem?

5. Considerando o trecho de imagem anterior, qual deve ser o novo valor do pixel central caso seja aplicado um Filtro de Média, um Filtro de Mediana e um Filtro Gaussiano (\(\sigma = 1,4\))?

6. Considerando uma imagem de dimensões n x n, como seria o código em Julia necessário para implementar o processo de convolução de uma máscara 3 x 3?

7. Qual a diferença entre filtros passa-baixa e passa-alta?

8. Qual a implicação da aplicação do Filtro de Sobel?

9. O que é filtragem adaptativa?

References

R. C. GONZALEZ, R. C. WOODS. 2010. Processamento Digital de Imagens. 3ª Edição. São Paulo, São Paulo: Pearson Prentice Hall.

P. R. MENESES, T. ALMEIDA. 2012. Introdução Ao Processamento de Imagens de Sensoriamento Remoto. 1ª Edição. Brasília, Distrito Federal: Universidade de Brasília.

O. MARQUES FILHO, H. VIEIRA NETO. 1999. Processamento Digital de Imagens. 1ª Edição. Rio de Janeiro, Rio de Janeiro: Brasport.

P. A. REGALIA. 2005. “Review of Fundamentals of Adaptive Filtering” Vol. 25 (No. 4). IEEE Control Systems Magazine.