Capítulo 3 Morfologia Matemática

Um tema muito estudado entre as técnicas de processamento de imagens é a morfologia matemática, que vêm apresentando resultados muito interessantes no preparo de fotografias para posterior análise.

O princípio básico da morfologia matemática aplicada a imagens é a extração de informações relativas à geometria e topologia de conjuntos desconhecidos, a partir do elemento estruturante, também conhecido como máscara (J. FACON 2011). Métodos como a erosão e a dilatação podem ser realizadas por máscaras de diferentes tamanhos, alterando a forma dos objetos da imagem. Combinando estes dois processos, obtêm-se ainda outros tantos como a abertura, fechamento, e etc.

3.1 Erosão

(R. C. GONZALEZ 2010) estabelece que a Erosão de A por B é definida como (Equação (3.1)):

\[\begin{equation} A \ominus B = \{z|(B)_z \cap A^c = \varnothing\} \tag{3.1} \end{equation}\]

Sendo A e B conjuntos de \(Z^2\).

O efeito prático do processo morfológico chamado erosão consiste na modificação das feições da imagem, diminuindo-as em seu entorno, literalmente “erodindo-as”. Tal efeito pode ser alcançado através de um filtro, onde o menor valor dos pixel recobertos pela máscara assume o valor do pixel filtrado. Consiste basicamente de um Filtro de Mínimo. A Figura 3.1 demonstra o efeito da Erosão em uma imagem sintética.

Figura 3.1: Efeito alcançado pela aplicação do operador morfológico de Erosão em uma imagem. Imagem sintética original (a); e Imagem erodida (b).

Para uma melhor exemplificação dos efeitos de tal operador morfológico, na Figura 3.2 é demonstrado o efeito desta ferramenta em uma imagem orbital. Nota-se que, apesar de pequeno, há um ligeiro aumento das áreas mais escuras pertencentes à cena.

Figura 3.2: Efeito alcançado pela aplicação do operador morfológico de Erosão em uma imagem orbital de 1000 x 1000 pixels. Imagem orbital original (a); e Imagem erodida por máscara 3 x 3 (b).

No âmbito desta biblioteca, tal operador pode ser aplicado através da função erosion_( ).

3.2 Dilatação

De forma semalhante à equação (3.1), (R. C. GONZALEZ 2010) também estabelece que a Dilatação de um conjunto A por B é definida como (Equação (3.2)):

\[\begin{equation} A \oplus B = \{z|(\hat{B})_z \cap A \neq \varnothing \} \tag{3.2} \end{equation}\]

O efeito prático do processo morfológico chamado Dilatação consiste na modificação das feições da imagem, aumentando-as em seu entorno. O filtro implementado adota o menor valor dos pixel recobertos pela máscara como o novo valor do pixel filtrado. Consiste basicamente de um Filtro de Máximo. A Figura 3.3 demonstra o efeito da Dilatação em uma imagem sintética.

Figura 3.3: Efeito alcançado pela aplicação do operador morfológico de Diltação em uma imagem. Imagem sintética original (a); e Imagem dilatada (b).

O efeito da Dilatação pode ser visto também na Figura 3.4, onde tal operador morfológico foi aplicado a uma imagem orbital. Nota-se que, apesar de pequeno, há um ligeiro aumento das áreas mais claras pertencentes à cena.

Figura 3.4: Efeito alcançado pela aplicação do operador morfológico de Dilatação em uma imagem orbital de 1000 x 1000 pixels. Imagem orbital original (a); e Imagem dilatada por máscara 3 x 3 (b).

No âmbito desta biblioteca, tal operador pode ser aplicado através da função dilation_( ).

3.3 Gradiente Morfológico

O Gradiente Morfológico (GM) de uma imagem A por uma máscara B é definido por (R. C. GONZALEZ 2010) de acordo com a Equação (3.3):

\[\begin{equation} GM = (A \oplus B ) - (A \ominus B) \tag{3.3} \end{equation}\]

Ou seja, nada mais é do que o resultado da Dilatação menos o resultado da Erosão. A Figura 3.5 exemplifica o resultado de tal operador morfológico em uma imagem sintética.

Figura 3.5: Efeito alcançado pela aplicação do operador morfológico Gradiente Morfológico em uma imagem sintética. Imagem original (a); e Resultado da aplicação do operador (b).

Para exemplificar os efeitos de tal operador morfológico em imagens orbitais, é mostrado na Figura 3.6 como age tal operador na mesma imagem orbital vista nas Figuras 3.2 e 3.4.

Figura 3.6: Efeito alcançado pela aplicação do Gradiente Morfológico em uma imagem orbital de 1000 x 1000 pixels. Imagem orbital original (a); e Imagem resultado da aplicação do Gradiente Morfológico com uma máscara 3 x 3 (b).

Como pode ser visto, apenas as bordas das feições contidas na imagem são retornadas, em diferentes níveis de cinza. Ao aplicar um algoritmo de limiarização, como os descritos no próximo capítulo, podem ser obtidas informações das bordas dos objetos. Ainda assim, tais bordas podem ser muito “grossas” na imagem, o que pode ser caracterizado como fonte de incerteza nas informações. Para corrigir tal fonte de incertezas, basta aplicar outro operador morfológico chamado de Afinamento Morfológico que visa a redução de tais bordas já limiarizadas a linhas de largura igual a apenas 1 pixel.

No âmbito desta biblioteca, o operador de Gradiente Morfológico pode ser aplicado através da função grad_morf( ).

3.4 Afinamento Morfológico

O Afinamento Morfológico, como dito anteriormente, visa a redução dos objetos da cena a extruturas que possuem largura de apenas 1 pixel. De acordo com (R. C. GONZALEZ 2010), tal método é composto pela aplicação de várias transformadas hit-or-miss, definidas de acordo com a equação (3.4):

\[\begin{equation} A \otimes = A - (A \circledast B) \tag{3.4} \end{equation}\]

Sendo \(\otimes\) o afinamento e \(\circledast\) a transformada hit-or-miss. Nesta última, uma máscara pré-estabelecida é comparada com a região a ser transformada. Os termos sobrepostos pela máscara são comparados com a mesma, e caso haja uma compatibilidade entre ambas, diz-se que há um “hit”, e caso contrário, há um “miss”. No caso do “hit”, há uma mudança no valor do pixel, no caso do “miss”, o pixel permanece o mesmo.

Como diferentes máscaras podem ser usadas para gerar afinamentos diferentes, foi implementado nesta biblioteca o modelo mais genérico possível, usando um total de 8 diferentes máscaras (Figura 3.7).

Figura 3.7: (a) até (h) - Máscaras usadas nas transformadas hit-or-miss do Afinamento Morfológico implementado.

Para que haja uma compatibilidade do algoritmo com os dados de entrada, tal operador pode ser usado apenas com imagens binásrias, ou seja, com níveis de cinza iguais a apenas 0 e 1. Na Figura (fig:mascarashitmiss), onde se encontram os valores iguais a “X”, indicam que para estas posições, não importa qual seja o valor do pixel analisado.

O efeito da aplicação de tal operador é demonstrado pela Figura 3.8.

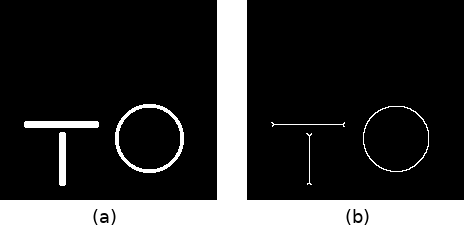
Figura 3.8: Imagem sintética binária (a); e Aplicação do afinamento morfológico (b).

3.5 Exercícios

1. Com o auxílio das funções erosion_() e dilation_() obtenha o resultado para a Erosão e Dilatação em uma imagem de seu computador. Depois disso faça uma subtração simples entre as duas. Descreva o resultado alcançado. (Dica: Use a função convert(Array{Float32}, convert(Array{Grey}, sua_imagem)) para converter sua imagem em uma matriz antes do processo, e depois a função imshow() da bibioteca ImageView para visualizar o resultado final).

2. Qual a diferença básica entre a Erosão e a Dilatação?

3. Como é feito o Gradiente Morfológico?

4. O que acontece com as feições de uma imagem que passa pelo processo de Afinamento Morfológico?

References

J. FACON. 2011. “A Morfologia Matemática E Suas Aplicações Em Processamento de Imagens” Capítulo 2 (p. 61-128). VII Workshop de Visão Computacional – WVC 2011.

R. C. GONZALEZ, R. C. WOODS. 2010. Processamento Digital de Imagens. 3ª Edição. São Paulo, São Paulo: Pearson Prentice Hall.