Capítulo 4 Limiarização

O processo de Limiarização compreende uma transformação dos níveis de cinza de uma imagem. Dados que todos os pixels são compostos por uma determinada magnitude dentro de um espectro, na Limiarização é escolhido um nível de cinza como limiar, para que então todos os níveis acima sejam substituídos pelo valor máximo, e abaixo deste nível pelo valor de mínimo. Matematicamente, (R. C. GONZALEZ 2010) define a Limiarização como (Equação (4.1)):

\[\begin{equation} g(x,y) = \left\{\begin{matrix} 1 \thinspace \thinspace \thinspace \thinspace \text{se} \thinspace \thinspace \thinspace \thinspace f(x,y)>T \\ 0 \thinspace \thinspace \thinspace \thinspace \text{se} \thinspace \thinspace \thinspace \thinspace f(x,y)\le T \end{matrix}\right. \tag{4.1} \end{equation}\]

Sendo \(g(x,y)\) a imagem resultante da imagem \(f(x,y)\), \(T\) é o nível escolhido para a Limiarização, e 1 o valor máximo e 0 o valor mínimo. O resultado, a imagem \(g(x,y)\), é então uma imagem binarizada.

4.1 Limiarização pela Mediana

O processo de Limiarização Pela Mediana é um dos mais simples de ser implementados. Como dito anteriormente, na limiarização é escolhido um valor de nível de cinza que servirá como divisor dos níveis de cinza que adotarão a cor branca dos que adotarão a cor preta. Como o próprio nome deixa implícito, o critério empregado é a utilização do valor de mediana entre os pixels de toda a imagem para escolher o valor de \(T\) referente à Equação (4.1).

Tomando uma imagem orbital já filtrada com o Operador de Sobel como exemplo, o resultado da aplicação deste tipo de limiarização é demonstrado através da Figura 4.1.

Imagem orbital filtrada pelo Operador de sobel (a) e aplicação da Limiarização pela Mediana (b).

Figura 4.1: Imagem orbital filtrada pelo Operador de sobel (a) e aplicação da Limiarização pela Mediana (b).

4.2 Limiarização de Otsu

O Método de Otsu para a limiarização pode ser considerado como uma ferramenta para a definição de um nível ótimo para o limiar, visto que não é afetado pela subjetividade do usuário. Tal método pode ser definido da seguinte forma (N. Otsu 1979), (R. C. GONZALEZ 2010):

  1. Calcular o histograma normalizado da imagem de entrada. Designar os componentes do histograma como \(p_i\), \(i = 0, 1, 2, \cdots, L-1\).

  2. Calcular as comas acumuladas, \(P_1 (k)\), para \(k = 0, 1, 2, \cdots, L-1\).

  3. Calcular as médias acumuladas, \(m(k)\), para \(k = 0, 1, 2, \cdots, L-1\).

  4. Calcular a intensidade média global, \(m_G\).

  5. Calcular a variância entre classes, \(\sigma_B^2(k)\), para \(k = 0, 1, 2, \cdots, L-1\).

  6. Obter o limiar de Otsu, \(k*\), como o valor de \(k\). Se a máxima não for única, obter \(k*\) pela média dos valores de \(k\) que correspondem aos diversos valores máximos detectados.

  7. Obter a medida de separabilidade, \(\eta *\), avaliando \(\eta (k) = \frac{\sigma_B^2(k)}{\sigma_G^2}\) em \(k=k*\).

A Figura 4.2 demonstra os efeitos alcançados por tal operação dada uma imagem orbital já filtrada pelo Operador de Sobel.

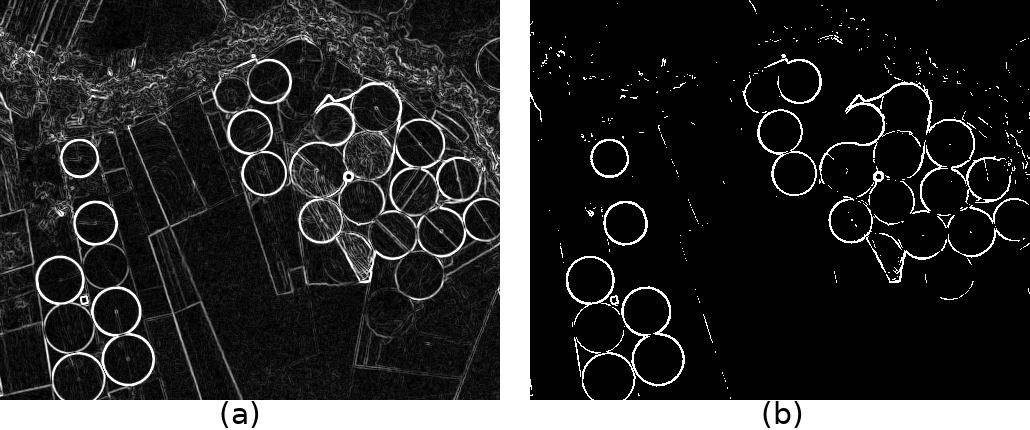
Imagem orbital filtrada pelo Operador de sobel (a) e aplicação da Limiarização pelo Método de Otsu (b).

Figura 4.2: Imagem orbital filtrada pelo Operador de sobel (a) e aplicação da Limiarização pelo Método de Otsu (b).

A função designada para tal processo é otsu_threshold_().

4.3 Exercícios

  1. Qual a definição matemática para o processo de limiarização?

  2. Qual o resultado encontrado após aplicar a Limiarização pela Mediana duas vezes seguidas na mesma imagem?

  3. Cite as etapas que definem o Método de Limiarização de Otsu.

N. Otsu. 1979. “A Threshold Selection Method from Gray Level Histograms” Vol. 9 (No. 1). IEEE transactions on systems, man,; cybernetics.

R. C. GONZALEZ, R. C. WOODS. 2010. Processamento Digital de Imagens. 3ª Edição. São Paulo, São Paulo: Pearson Prentice Hall.

References

R. C. GONZALEZ, R. C. WOODS. 2010. Processamento Digital de Imagens. 3ª Edição. São Paulo, São Paulo: Pearson Prentice Hall.

N. Otsu. 1979. “A Threshold Selection Method from Gray Level Histograms” Vol. 9 (No. 1). IEEE transactions on systems, man,; cybernetics.